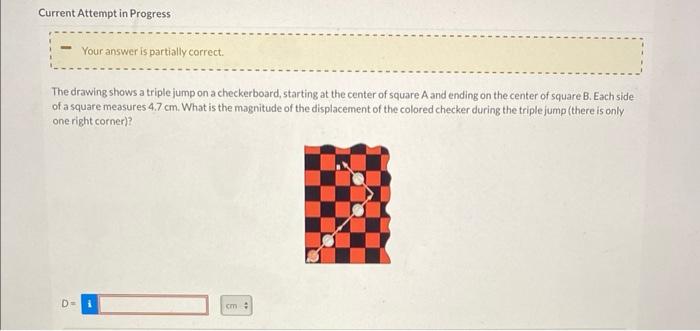
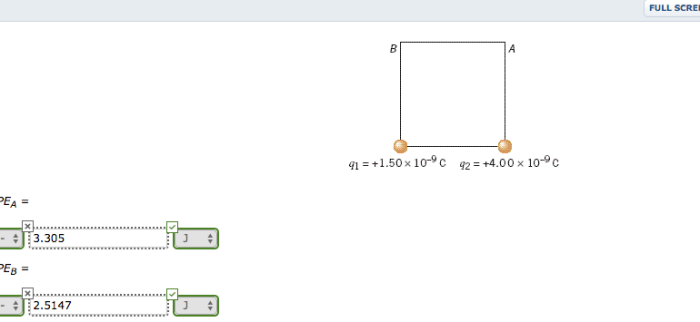
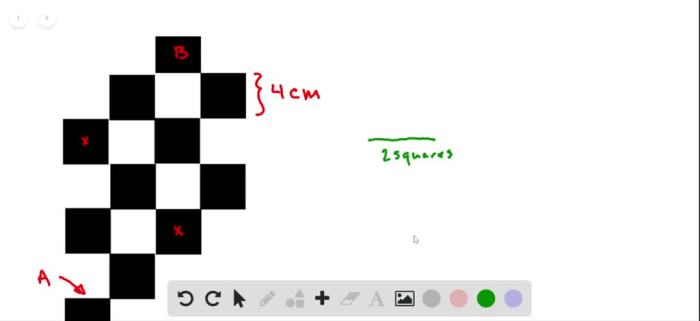
The drawing shows a square each side of which – The drawing shows a square, a geometric shape with four equal sides and four right angles, setting the stage for an exploration of its intriguing properties and diverse applications. From its fundamental role in geometry and mathematics to its practical uses in architecture, design, and engineering, the square holds a unique place in our understanding of the world around us.
This comprehensive overview will delve into the visual representation of the square, examining the significance of drawings in conveying geometric information. We will explore formulas and methods for calculating its perimeter and area, unravel the relationship between its side length and these measurements, and uncover the properties of its diagonals.
Introduction to the Square
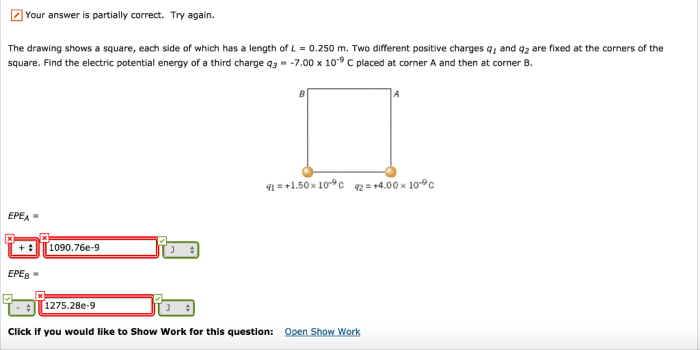
A square is a two-dimensional geometric shape with four equal sides and four right angles. It is a regular quadrilateral, meaning that all of its sides and angles are equal. Squares are significant in geometry and mathematics due to their simple and symmetrical properties.
Visual Representation of the Square
The drawing provided depicts a square, with each side of equal length. Visual representations, such as drawings and diagrams, are crucial for understanding geometric shapes. They provide a concrete representation that helps visualize the properties and relationships within the shape.
Drawings have the advantage of being easily understood and allowing for quick visualization of the shape. However, they can be limited in conveying precise measurements or complex geometric relationships.
Measurement and Properties of the Square, The drawing shows a square each side of which
The perimeter of a square is the sum of the lengths of all four sides. The formula for calculating the perimeter is P = 4s, where P is the perimeter and s is the length of one side.
The area of a square is the measure of the enclosed space within the square. The formula for calculating the area is A = s 2, where A is the area and s is the length of one side.
Diagonals are line segments that connect opposite vertices of a square. The diagonals of a square are equal in length and perpendicular to each other. The point of intersection of the diagonals divides each diagonal into two equal segments.
Applications of Squares in Real-World Scenarios
Squares are widely used in architecture, design, and engineering due to their stability and aesthetic appeal. Buildings, bridges, and other structures often incorporate square elements to provide support and balance.
In design, squares are used to create patterns, grids, and logos. They provide a sense of order and symmetry, making them visually pleasing and easy to recognize.
Squares also play a role in everyday life, such as in the design of tiles, building blocks, and grids for organizing information. Their simple and recognizable shape makes them a versatile tool for solving real-world problems.
FAQ Compilation: The Drawing Shows A Square Each Side Of Which
What is the definition of a square?
A square is a two-dimensional shape with four equal sides and four right angles.
How do I calculate the perimeter of a square?
To calculate the perimeter of a square, multiply the length of one side by 4.
What is the significance of squares in architecture?
Squares are commonly used in architecture due to their stability, symmetry, and aesthetic appeal.